机器学习大作业——手写汉字识别

2023-07-03

考核说明

总成绩构成：

出勤（10%）+ 课节作业（50%） + 项目大作业（40%）

项目大作业

考核要求：

选定一个适用机器学习技术来解决的现实问题，运用所学的机器学习手段及方法构建一个完整的项目。要包含完整的机器学习要素：任务介绍及机器学习术语描述，数据集中的样本及标签解读，模型设计原理，损失函数设计，优化方法，代码实现，实验结果及分析。

呈现形式：

书面报告：在本文档中完成，直接提交 notebook 电子文件到 AIstudio 云平台上，项目内容解读使用 Markdown 模块，项目代码使用 Code 模块，以及代码模块的运行结果
现场讲解及答辩。

评分标准：

将按照考核要求中的要素的完整性进行评分，主要评估机器学习要素解读的正确性，完整性，以及项目解决方案设计的启发性。评分详细条目及分值分配如下表所示：

任务介绍 (5 分)	数据集描述 (5 分)	模型分析 (20 分)	损失函数分析 (10 分)	优化方法 (5 分)
得分	得分	得分	得分	得分

代码实现 (30 分)	实验结果及分析 (10 分)	现场讲解及答辩 (15 分)
得分	得分	得分

注意

提交大作业时，同时上传查重报告，以避免抄袭。
不允许贴图文本块以及公式块，务必手工录入。

1.任务介绍

去年我的母亲想要把一张手写的合同录入到电脑中打印下来，但是她并不会使用电脑，因此就找到了我，我的第一想法就是qq自带的图片识别文字的功能，但是由于手写的实在是有点乱，识别的效果并不好，最终还是手打了一份。如今，我想通过机器学习的SVM模型去尝试着实现手写汉字识别，并尽可能达到一个好的效果。
本次大作业中，我先后尝试了SVM与KNN两种方法对手写汉字进行识别，并尝试通过PCA降维提高准确率。

2.数据集描述

中科院自动化研究所-手写中文数据集
数据来源：http://www.nlpr.ia.ac.cn/databases/handwriting/Download.html
包含在线和离线两类手写数据，HWDB1.0~~1.2总共有3895135个手写单字样本，分属7356类（7185个汉字和171个英文字母、数字、符号）；HWDB2.0~~2.2总共有5091页图像，分割为52230个文本行和1349414个文字。所有文字和文本样本均存为灰度图像。
使用建议：数据为单字，白色背景，可以大量合成文字行进行训练。白色背景可以处理成透明状态，方便添加各种背景。对于需要语义的情况，建议从真实语料出发，抽取单字组成文字行

3.模型分析

3.1 主要思想

SVM模型的主要采用最大化最小几何间隔的思想，即尽力让边界附近的样本不仅保持在各自应属的一边，并且距离边界越远越好。SVM的学习目标就是找到一个决策超平面，使得训练样本集到超平面的最小距离最大化。

3.2 SVM方法

3.2.1 硬间隔SVM

当训练样本线性可分时，可以直接通过硬间隔最大化学习一个线性可分支持向量机。但是当特征维度很大时，这种方式计算效率低，耗费内存大。为了求解线性可分支持向量机的最优化问题，将它作为原始最优化问题，应用拉格朗日对偶性，通过求解对偶问题（dual problem）得到原始问题（primal problem）的最优解。

3.2.2 软间隔SVM

对于决策边界近似线性的数据，可以使用软间隔的方法，允许数据跨越决策面（允许误分类），但是需要对跨越决策面的数据加以惩罚。对于复杂决策面的数据，则通过核函数的方法将低维数据映射到高维甚至无限维空间，将低维线性不可分的数据转换成高维线性可分的数据，进而化简决策问题。

3.2.3 核函数与核方法

对于线性不可分的数据，可以引入核函数。核方法的基本原理是把原坐标系里线性不可分的数据使用核函数（Kernel）投影到另一个空间，尽量使得数据在新的空间里线性可分。核函数方法的广泛应用, 有以下特点或用途：

核函数的引入避免了“维数灾难”,大大减小了计算量。而输入空间的维数n对核函数矩阵无影响，因此，核函数方法可以有效处理高维输入。
无需知道非线性变换函数的形式和参数。
核函数的形式和参数的变化会隐式改变从输入空间到特征空间的映射，进而对特征空间的性质产生影响，最终改变各种核函数方法的性能。
核函数方法可以和不同的算法相结合，形成多种不同的基于核函数技术的方法，且这两部分的设计可以单独进行，并可以为不同的应用选择不同的核函数和算法。

3.3 项目分析

KNN主要适用于准确度要求不那么高，样本较少的情况。SVM适用于对正确率有着比较高的要求，样本比较多的情况。并且KNN不能处理样本维度太高的东西，SVM处理高纬度的数据比较优秀。对于手写汉字识别这个目标来说，汉字有很多很多，并且对于识别的正确率也有着很高的要求，因此KNN就不适用了，选择SVM模型。并且由于汉字图片线性不可分，因此需要使用核函数，这里选择了高斯核函数（Gaussian Kernel），在SVM中也称为径向基核函数（Radial Basis Function,RBF），它是非线性分类SVM最主流的核函数。
同时在图片预处理中，也可以使用PCA降维的方法来提取主要特征，尝试是否能提高准确率。最后也可以使用KNN做一个对比。

4 损失函数分析

SVM的损失函数为Hinge loss，对此共有两种解读观点。

4.1 第一种解读观点

优化目标中关注的是变量ξ的最小值，从变量ξ的角度来审视一下两个约束条件，可以描述为
$\xi_i\ge1-y_i(w^T+b),i=1,2,…,N$
$\xi_i\ge0,i=1,2,…,N$
可以看出，这两个不等式同时约束了松弛变量ξ的下界，因此，要求这两个约束不等式约束条件下的ξ的最小值，则只需要最小化下界中的较大的下界即可，即为：
$min max{0,1-y_i(w^Tx_i+b)}$
所以软支持向量的优化问题可以描述为：$min[\frac 12w^Tw+\sum_{i=1}^Nmax{0,1-y_i(w^Tx_i+b)}]$
所以损失函数为$max{0,1-y_i(w^Yx_i+b)}$，第一项可以看作是模型参数的$L_2$范数正则化项。

4.2 第二种解读观点

直接令$\xi_i=max{0,1-y_i(w^Tx_i+b)}$则，可以看出$\xi_i\ge0$，所以软支持向量机优化问题中的第二个约束条件恒成立。当$1-y_i(w^Tx_i+b)>0$时，则$max{0,1-y_i(w^Tx_i+b)}=1-y_i(w^Tx_i+b)\equiv\xi_i$，即$y_i(w^Tx_i+b)=1-\xi_i$
当$1-y_i(w^Tx_i+b)\le0$，则$max{0,1-y_i(w^Tx_i+b)}=0\equiv\xi_i$，即$\xi_i=0$，所以$1-y_i(w^Tx_i+b)\le\xi_i$，即$y_i(w^Tx_i+b)\ge1-\xi_i$
综合上述两种情况，软支持向量机优化问题中的第一个约束条件恒成立。因此软支持向量的优化问题可以描述为如下无约束优化问题（这也是SVM的另一种新的形式化描述，侧重于体现损失函数，但不具有优化求解的便利性）：$min[\frac 12w^Tw+\sum_{i=1}^Nmax{0,1-y_i(w^Tx_i+b)}]$
所以，损失函数为$max{0,1-y_i(w^Tx_i+b)}$，第一项可以看做是模型参数的$L_2$范数正则化项。该损失函数在业界内有一个名字，即所谓的铰链损失。

5 优化方法

5.1 SMO算法

基本思想：如果所有$\alpha$（每一个样本都对应着一个$\alpha$）都满足最优化问题的KKT条件，那么这个最优化问题的解就得到了。
SMO算法尝试将原始的二次规划问题分解为一个个小的二次规划问题。SMO算法首先选择两个违背KKT条件最严重的α，并固定其它α，针对这两个α构造一个二次规划问题，重复该过程，直到所有的α都满足KKT条件。这样得到的解就更接近原始的二次规划问题的解。具体地，SMO算法在初始化所有的变量αi,i=1,2,…,n之后，不断执行下述三个步骤，直到收敛：

根据一定的启发式策略（如预测误差的差值最大的两个样本对应的α），选取两个优化变量αi和αj
将其他的变量当做常数，求解只有αi和αj两个变量的最优化问题 3、更新αi和αj，如果变量收敛，则停止；否则，重复步骤1
由SMO算法可得出所有α值，如何根据对偶问题的解α反推原问题的解w和b?
首先，根据前述拉格朗日函数对w偏导公式，可知$w=\sum_{i}\alpha_iy_ix_i$。
那么如何求b呢？此处需要用到KKT条件。根据KKT条件，原问题的最优解w⋆满足下述条件
$\alpha^*_i\ge0$
$y_i(w^{T}x_i+b^)\ge1$
$\alpha^*_i(y_i(w^{T}x_i+b^)-1)=0$

5.2 对偶问题

构建拉格朗日法将原问题转换成无约束的最优化问题，拉格朗日函数(w,b)可以写成：$L(w,b,\alpha)=\frac 12||w||^2-\sum_{i}\alpha_i(y_i(w^Tx_i+b)-1)$
现在我们的问题为：$min_{w,b}max_{\alpha_i\ge0}L(w,b,\alpha)$，由于问题时凸二次规划问题，且满足Slater条件，因此上述问题等价于$max_{\alpha_i\ge0}min_{w,b}L(w,b,\alpha)$
当原问题转化为对偶问题之后，想要原问题的解与对偶问题的解等价，即通过求对偶问题的解可以得到原问题的解，则需要满足KKT条件。首先，需要满足KKT条件的第一个条件。求解内部的最小化问题，将拉格朗日函数分别对w和b求偏导，并令偏导为零，有：
$\frac{\partial L(w,b,\alpha)}{\partial w}=w-\sum_{i}\alpha_iy_ix_i=0\Rightarrow w=\sum_{i}\alpha_iy_ix_i$
$\frac{\partial L(w,b,\alpha)}{\partial b}=-\sum_{i}\alpha_iy_i=0\Rightarrow \sum_{i}\alpha_iy_i=0$
将$w=\sum_{i}\alpha_iy_ix_i$代入拉格朗日函数，则我们的优化目标等价于$L(w,b,\alpha)=\sum_{i}\alpha_i-\frac 12\sum_{i}\sum_{j}\alpha_i\alpha_j y_i y_j(x^T_ix_j)$
此时，我们的最优化问题等价于
$max_{\alpha_i\ge0}\sum_{i}\alpha_i-\frac 12\sum_{i}\sum_{j}\alpha_i\alpha_j y_i y_j(x^T_ix_j)$
s.t.$\sum_{i}\alpha_iy_i=0$

6.代码实现

6.1 解压缩数据集并读入数据标签

# 导入模块
import numpy as np
import glob
from PIL import Image
import random
import matplotlib.pyplot as plt
# from sklearn.externals import joblib
from sklearn.svm import SVC
import joblib
from sklearn.neighbors import KNeighborsClassifier
import pandas as pd


import os
import zipfile
os.chdir('/home/aistudio/')
extracting = zipfile.ZipFile('train.zip')
extracting.extractall()


# 读入table文件
path_ = 'train/'
f=open('汉字对照表.txt', encoding='gbk')
txt=[]
classes = []
table = []
cnt=0
for line in f:
    cnt=cnt+1
    #选择训练多少个汉字
    if cnt>10:
        break
    txt=line.strip().split(' ')
    classes.append(txt[0])
    table.append(txt[1])
print(classes)
print(table)

['00000', '00001', '00002', '00003', '00004', '00005', '00006', '00007', '00008', '00009']
['一', '丁', '七', '万', '丈', '三', '上', '下', '不', '与']

6.2 读取手写汉字图片数据

#二维列表，[手写汉字的图片信息，汉字的编号]
infolist = []
#遍历训练数据集，将数据读入infolist
for index, name in enumerate(classes):
    #构造路径
    path = path_ + str(name) + '/'
    path = glob.glob(path + '*.png')
    for img_name in path:
        #将图片转成灰度图，并统一大小为14*14，再转为16色
        img = Image.open(img_name)
        img = img.convert('L')
        img = img.resize((14,14))
        img = img.point(lambda i: (255-i)//16)
        data_i = [np.array(img).flatten().tolist(), index]
        infolist.append(data_i)

6.3 使用PCA，观察不同维度下的方差占比

from sklearn.decomposition import PCA
#尝试使用PCA降维，是否能提高准确率

#二维列表，[手写汉字的图片信息，汉字的编号]
infolist = []
imglist = []

#遍历训练数据集，将数据读入infolist
for index, name in enumerate(classes):
    #构造路径
    path = path_ + str(name) + '/'
    path = glob.glob(path + '*.png')
    for img_name in path:
        #将图片转成灰度图，并统一大小为14*14，再转为16色
        img = Image.open(img_name)
        img = img.convert('L')
        img = img.resize((14,14))
        img = img.point(lambda i: (255-i)//16)
        data_i = [np.array(img).flatten().tolist(), index]
        infolist.append(data_i)

infolist = np.array(infolist)
# 加载数据 
#X=np.array(infolist[:,0])
X = [np.array(i[0]) for i in infolist]
y = infolist[:,1]


component_list=[5,20,50,100,150,196]
# pca降维过程
for i in component_list:
    pca = PCA(n_components=i)
    X_pca = pca.fit_transform(X)
    # 计算第一主成分方差占比
    ratio_sum =np.sum(pca.explained_variance_ratio_)
    ratio_acc=0
    ratio_list=[]
    for j in pca.explained_variance_ratio_:
        ratio_acc=ratio_acc+j
        ratio_list.append(ratio_acc/ratio_sum)
    fig = plt.figure()
    plt.bar(np.arange(len(ratio_list)),ratio_list,0.5,color="green")
    plt.title('n_components='+str(i))
    plt.xlabel('ratio')
    plt.ylabel('ratio_acc')
    plt.plot()

/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/ipykernel_launcher.py:22: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray.
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
  (prop.get_family(), self.defaultFamily[fontext]))

png

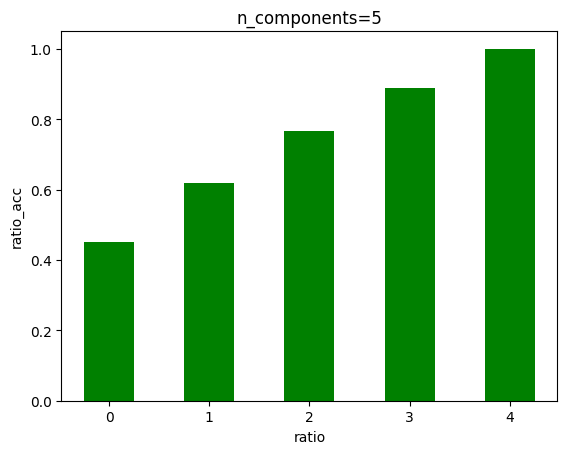
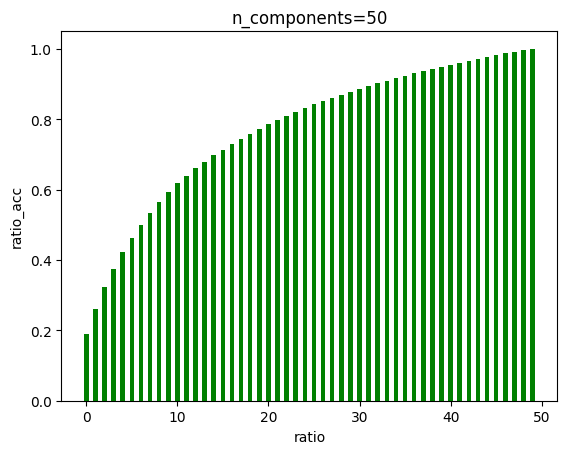
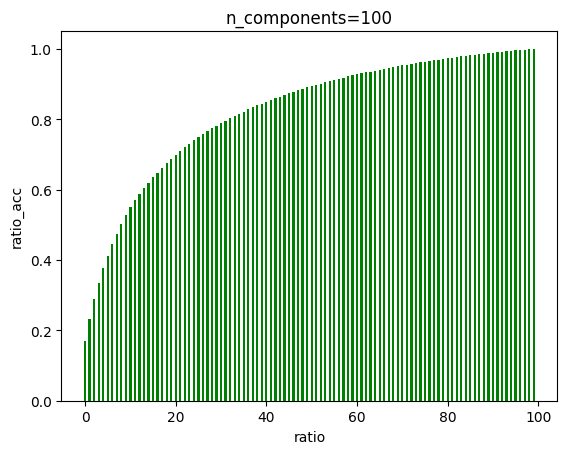
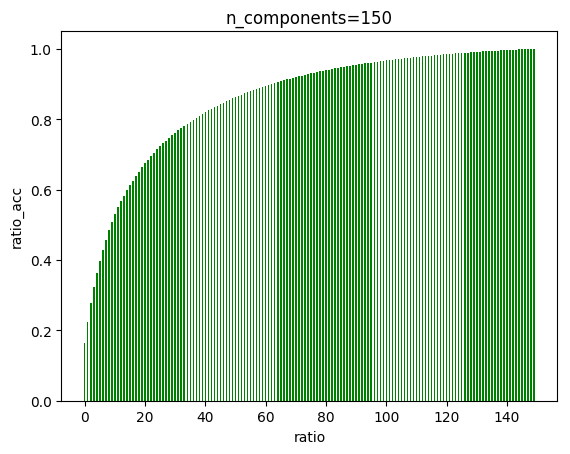
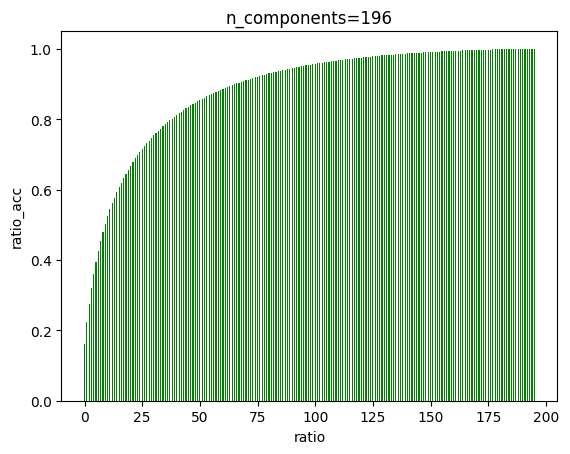
6.4 由PCA降维图可以看出，在大概135左右，曲线趋近于一条直线，我们可以降维至135

import numpy.linalg as LA
X = [np.array(i[0]) for i in infolist]
y = infolist[:,1]

X=np.mat(X)
def pca(dataMat, n_components):
    
    # 数据中心化
    meanVals = np.mean(dataMat, axis=0)
    centered =  dataMat - meanVals
    
    # 计算协方差矩阵，并进行特征值分解
    # 注意，协方差矩阵计算需指定rowvar参数为False，即表明每一列
    # 为每一个特征的不同取值
    covMat = np.cov(centered, rowvar=False)
    w, v = LA.eig(covMat)
    # 将特征值从大到小排序，并得到对应的索引值序列
    idxMin2Max = np.argsort(w)
    idxMax2Min = idxMin2Max[::-1]
    
    # 取前n_components个特征向量构成转换矩阵
    vidx = idxMax2Min[:n_components]
    tfMat = v[:, vidx]
    
    # 将原始数据转换到新的低维空间
    lowdMat = np.matmul(centered, tfMat)
    return lowdMat, tfMat,w,v


n_components = 135
# pca降维
lowdMat, tfMat, w, v = pca(X, n_components=n_components)
# 计算重构误差
meanVal = np.mean(X, axis=0)  # 均值

#reconMat =np.mat(lowdMat)*np.mat(tfMat.T)+np.mat(meanVal)  # 重构数据
#reconMat=p.inverse_transform(lowdMat)#s重构数据

secon_centered=X-meanVal
reconMat =np.matmul(lowdMat,tfMat.T)  # 重构数据
errMat = secon_centered-reconMat # 残差
froerr =LA.norm(errMat,'fro')  # Frobenius范数计算
print("残差的Frobenius范数：")
print(froerr)
froerrSquare =froerr*froerr
print("重建误差：残差的Frobenius范数的平方：")
print(froerrSquare)

残差的Frobenius范数：
220.32679427894584
重建误差：残差的Frobenius范数的平方：
48543.89627723692

6.5 使用原始数据进行训练测试

#二维列表，[手写汉字的图片信息，汉字的编号]
infolist = []
#遍历训练数据集，将数据读入infolist
for index, name in enumerate(classes):
    #构造路径
    path = path_ + str(name) + '/'
    path = glob.glob(path + '*.png')
    for img_name in path:
        #将图片转成灰度图，并统一大小为14*14，再转为16色
        img = Image.open(img_name)
        img = img.convert('L')
        img = img.resize((14,14))
        img = img.point(lambda i: (255-i)//16)
        data_i = [np.array(img).flatten().tolist(), index]
        infolist.append(data_i)
random.shuffle(infolist)

# 获取X，Y
infolist = np.array(infolist)

img = infolist[:, 0]
label = infolist[:, 1]
img = img.tolist()
label = label.tolist()
# print(img)
# print(label)
X = img
Y = label

# 划分数据集
split_index = 5 * len(Y) // 6
x_train, x_test = X[:split_index], X[split_index:]
y_train, y_test = Y[:split_index], Y[split_index:]
print("训练数据格式:{}".format(np.shape(x_train)))
print("测试数据格式:{}".format(np.shape(x_test)))

#加载已经训练好的模型
#algo=joblib.load("svm.pkl")

# 模型效果查看
result_train=[]
result_test=[]
for i in range(80,101,2):
    # 构建模型
    algo = SVC(kernel='rbf', C=i/100)
    algo.fit(x_train, y_train)
    result_train.append(round(algo.score(x_train, y_train),3))
    result_test.append(round(algo.score(x_test, y_test),3))
print(result_train)
print(result_test)
font = font_manager.FontProperties(fname='MSYHL.TTC')

plt.plot(0)
plt.bar(np.arange(80,101,2)/100,result_train,0.01,color="green")
plt.title('SVM Accuracy')
plt.xlabel('惩罚系数C', fontproperties=font)
plt.ylabel('训练集上准确率', fontproperties=font)
plt.xlim(0.8,1.0)#y轴范围设置
plt.ylim(0.8,1.0)#y轴范围设置
plt.show()

plt.plot(1)
plt.title('SVM Accuracy')
plt.bar(np.arange(80,101,2)/100,result_test,0.01,color="green")
plt.xlabel('惩罚系数C', fontproperties=font)
plt.ylabel('测试集上准确率', fontproperties=font)
plt.xlim(0.8,1.0)#y轴范围设置
plt.ylim(0.8,1.0)#y轴范围设置
plt.show()

# 模型持久化
joblib.dump(algo, './svm.pkl')

/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/ipykernel_launcher.py:19: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray.


训练数据格式:(1984, 196)
测试数据格式:(397, 196)
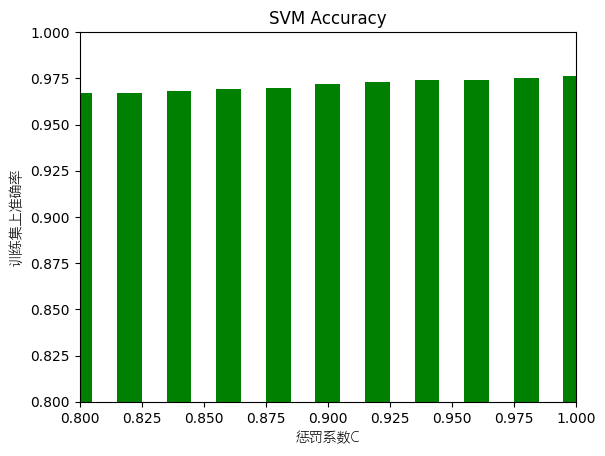
[0.967, 0.967, 0.968, 0.969, 0.97, 0.972, 0.973, 0.974, 0.974, 0.975, 0.976]
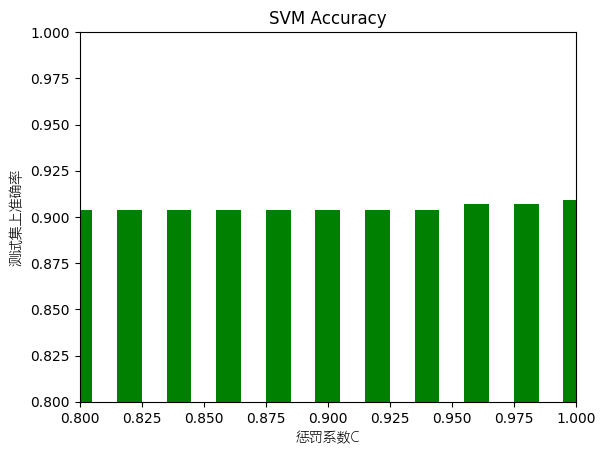
[0.904, 0.904, 0.904, 0.904, 0.904, 0.904, 0.904, 0.904, 0.907, 0.907, 0.909]


/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
  (prop.get_family(), self.defaultFamily[fontext]))

png

['./svm.pkl']

6.6 使用降维重建后的数据进行训练测试

import numpy.linalg as LA
from matplotlib import font_manager
#二维列表，[手写汉字的图片信息，汉字的编号]
infolist = []
#遍历训练数据集，将数据读入infolist
for index, name in enumerate(classes):
    #构造路径
    path = path_ + str(name) + '/'
    path = glob.glob(path + '*.png')
    for img_name in path:
        #将图片转成灰度图，并统一大小为14*14，再转为16色
        img = Image.open(img_name)
        img = img.convert('L')
        img = img.resize((14,14))
        img = img.point(lambda i: (255-i)//16)
        data_i = [np.array(img).flatten().tolist(), index]
        infolist.append(data_i)

infolist = np.array(infolist)
X = [np.array(i[0]) for i in infolist]
y = infolist[:,1]
X=np.mat(X)
def pca(dataMat, n_components):
    
    # 数据中心化
    meanVals = np.mean(dataMat, axis=0)
    centered =  dataMat - meanVals
    
    # 计算协方差矩阵，并进行特征值分解
    # 注意，协方差矩阵计算需指定rowvar参数为False，即表明每一列
    # 为每一个特征的不同取值
    covMat = np.cov(centered, rowvar=False)
    w, v = LA.eig(covMat)
    # 将特征值从大到小排序，并得到对应的索引值序列
    idxMin2Max = np.argsort(w)
    idxMax2Min = idxMin2Max[::-1]
    
    # 取前n_components个特征向量构成转换矩阵
    vidx = idxMax2Min[:n_components]
    tfMat = v[:, vidx]
    
    # 将原始数据转换到新的低维空间
    lowdMat = np.matmul(centered, tfMat)
    return lowdMat, tfMat,w,v
n_components = 135
# pca降维
lowdMat, tfMat, w, v = pca(X, n_components=n_components)
# 计算重构误差
meanVal = np.mean(X, axis=0)  # 均值
reconMat =np.matmul(lowdMat,tfMat.T)+np.mat(meanVal)  # 重构数据
reconMat=reconMat.tolist()
infolist=[list(t) for t in zip(reconMat,list(y))]

# 打乱数据
random.shuffle(infolist)

# 获取X，Y
infolist = np.array(infolist)

img = infolist[:, 0]
label = infolist[:, 1]
img = img.tolist()
label = label.tolist()
# print(img)
# print(label)
X = img
Y = label

# 划分数据集
split_index = 5 * len(Y) // 6
x_train, x_test = X[:split_index], X[split_index:]
y_train, y_test = Y[:split_index], Y[split_index:]
print("训练数据格式:{}".format(np.shape(x_train)))
print("测试数据格式:{}".format(np.shape(x_test)))

#加载已经训练好的模型
#algo=joblib.load("svm_pca.pkl")
result_train=[]
result_test=[]
for i in range(80,101,2):
    # 构建模型
    algo = SVC(kernel='rbf', C=i/100, gamma=0.001)
    algo.fit(x_train, y_train)
    result_train.append(round(algo.score(x_train, y_train),3))
    result_test.append(round(algo.score(x_test, y_test),3))
print(result_train)
print(result_test)
font = font_manager.FontProperties(fname='MSYHL.TTC')

plt.plot(0)
plt.bar(np.arange(80,101,2)/100,result_train,0.01,color="green")
plt.title('SVM Accuracy')
plt.xlabel('惩罚系数C', fontproperties=font)
plt.ylabel('训练集上准确率', fontproperties=font)
plt.xlim(0.8,1.0)#y轴范围设置
plt.ylim(0.8,1.0)#y轴范围设置
plt.show()

plt.plot(1)
plt.title('SVM Accuracy')
plt.bar(np.arange(80,101,2)/100,result_test,0.01,color="green")
plt.xlabel('惩罚系数C', fontproperties=font)
plt.ylabel('测试集上准确率', fontproperties=font)
plt.xlim(0.8,1.0)#y轴范围设置
plt.ylim(0.8,1.0)#y轴范围设置
plt.show()


# 模型持久化
joblib.dump(algo, './svm_pca.pkl')

/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/ipykernel_launcher.py:19: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray.
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/ipykernel_launcher.py:58: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray.


训练数据格式:(1984, 196)
测试数据格式:(397, 196)
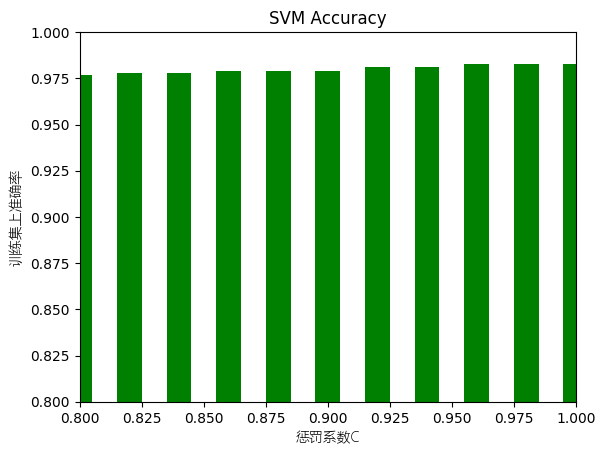
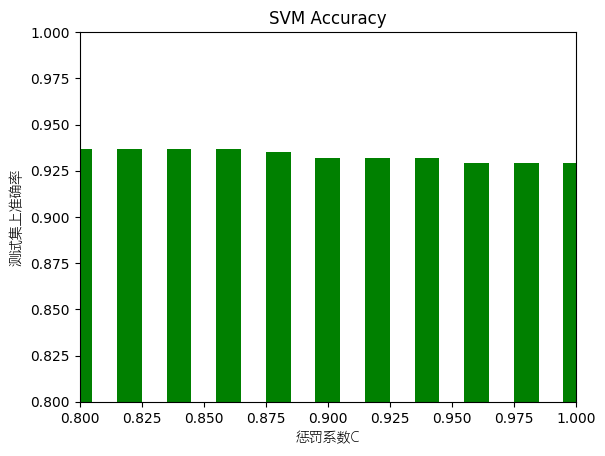
[0.977, 0.978, 0.978, 0.979, 0.979, 0.979, 0.981, 0.981, 0.983, 0.983, 0.983]
[0.937, 0.937, 0.937, 0.937, 0.935, 0.932, 0.932, 0.932, 0.929, 0.929, 0.929]


/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
  (prop.get_family(), self.defaultFamily[fontext]))

png

['./svm_pca.pkl']

6.7 混淆矩阵

from sklearn import svm
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from matplotlib import font_manager
# confusion matrix
font = font_manager.FontProperties(fname='MSYHL.TTC')

infolist = []
#遍历训练数据集，将数据读入infolist
for index, name in enumerate(classes):
    #构造路径
    path = path_ + str(name) + '/'
    path = glob.glob(path + '*.png')
    for img_name in path:
        #将图片转成灰度图，并统一大小为14*14，再转为16色
        img = Image.open(img_name)
        img = img.convert('L')
        img = img.resize((14,14))
        img = img.point(lambda i: (255-i)//16)
        data_i = [np.array(img).flatten().tolist(), index]
        infolist.append(data_i)

infolist = np.array(infolist)
img = infolist[:, 0]
label = infolist[:, 1]
img = img.tolist()
label = label.tolist()
# print(img)
# print(label)
X = img
Y = label


predictlist=algo.predict(X)
confusion= confusion_matrix(Y,predictlist)
plt.imshow(confusion, cmap=plt.cm.Blues)
 
# 热度图，后面是指定的颜色块，可设置其他的不同颜色
plt.imshow(confusion, cmap=plt.cm.Blues)
# ticks 坐标轴的坐标点
# label 坐标轴标签说明
indices = range(len(confusion))
# 第一个是迭代对象，表示坐标的显示顺序，第二个参数是坐标轴显示列表
# plt.xticks(indices, [0, 1, 2])
# plt.yticks(indices, [0, 1, 2])
plt.xticks(indices, range(10), fontproperties=font)
plt.yticks(indices, range(10), fontproperties=font)
 
plt.colorbar()
 
plt.xlabel('True Labels')
plt.ylabel('Predicted Labels')
plt.title('SVM Accuracy')
 
# plt.rcParams两行是用于解决标签不能显示汉字的问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 显示数据
for first_index in range(len(confusion)):  # 第几行
    for second_index in range(len(confusion[first_index])):  # 第几列
        plt.text(first_index, second_index, confusion[first_index][second_index])
# 在matlab里面可以对矩阵直接imagesc(confusion)
 
# 显示
plt.show()

/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/ipykernel_launcher.py:25: VisibleDeprecationWarning: Creating an ndarray from ragged nested sequences (which is a list-or-tuple of lists-or-tuples-or ndarrays with different lengths or shapes) is deprecated. If you meant to do this, you must specify 'dtype=object' when creating the ndarray.
/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
  (prop.get_family(), self.defaultFamily[fontext]))

png

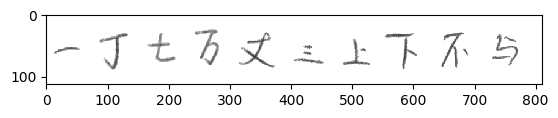
6.7 对包含一段话的图片进行字符切割，并预测这段话是什么

import numpy as np
import glob
from PIL import Image
import random
from sklearn.svm import SVC
import joblib
from matplotlib import pyplot as plt
%matplotlib inline
algo=joblib.load("svm.pkl")

import os
import cv2
import numpy as np

#需要分割图片的路径
origin_dir = "split/origin/"
#分割后图片的输出路径
dst_dir = "split/dest/"

#灰度值大于多少就认为有字
min_val = 20
#每个字的间隔
min_range = 10

count = 0
#水平或垂直分割图片，将起始位置和终止位置保存在peek_ranges中
def extract_peek(array_vals, minimun_val, minimun_range):
    #起始位置
    start_i = None
    #终止位置
    end_i = None
    peek_ranges = []
    for i, val in enumerate(array_vals):
        #如果start_i为空并且灰度值大于最小值就认为有字
        if val > minimun_val and start_i is None:
            start_i = i
        #还在这个字上
        elif val > minimun_val and start_i is not None:
            pass
        #这个字已经结束了，设置终点值
        elif val < minimun_val and start_i is not None:
            #如果空隔间距大于字的最小范围就认为是一个字
            if i - start_i >= minimun_range:
                end_i = i
                print(start_i,end_i)
                peek_ranges.append((start_i, end_i))
                start_i = None
                end_i = None
        elif val < minimun_val and start_i is None:
            pass
        else:
            raise ValueError("cannot parse this case...")
    return peek_ranges
#裁剪图片
def cutImage(img, peek_range):
    global count
    testlist=[]
    for i, peek_range in enumerate(peek_ranges):
        #竖直方向切割图片
        for vertical_range in vertical_peek_ranges2d[i]:
            x = vertical_range[0]
            y = peek_range[0]
            w = vertical_range[1] - x
            h = peek_range[1] - y
            pt1 = (x, y)
            pt2 = (x + w, y + h)
            count += 1
            img1 = img[y:peek_range[1], x:vertical_range[1]]
            new_shape = (80, 80)
            img1 = cv2.resize(img1, new_shape)
            # 模型效果查看
            cv2.imwrite(dst_dir + str(count) + ".png", img1)
            
            #预测切割出来的字是什么
            img1 = Image.open(dst_dir + str(count) + ".png")
            img1 = img1.convert('L')
            img1 = img1.resize((14, 14))
            img1 = img1.point(lambda i: (255-i)//16)
            img1 = np.array(img1).flatten().tolist()
            testlist.append(img1)
    predictlist=algo.predict(testlist)
    resultlist=[]
    for i in predictlist:
        resultlist.append(table[i])
    print("预测结果")
    print(resultlist)
    img = cv2.imread(origin_dir + fileName)
    plt.imshow(img)
            # cv2.rectangle(img, pt1, pt2, color)

#遍历需要分割的图片
for fileName in os.listdir(origin_dir):
    print(origin_dir + fileName)
    img = cv2.imread(origin_dir + fileName)
    #将图片转换为灰度图
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    
    #分离目标区域和背景区域
    #src：灰度化的图片
    #maxValue：满足条件的像素点需要设置的灰度值
    #adaptiveMethod：自适应方法。有2种：ADAPTIVE_THRESH_MEAN_C 或 ADAPTIVE_THRESH_GAUSSIAN_C
    #thresholdType：二值化方法，可以设置为THRESH_BINARY或者THRESH_BINARY_INV
    #blockSize：分割计算的区域大小，取奇数
    #C：常数，每个区域计算出的阈值的基础上在减去这个常数作为这个区域的最终阈值，可以为负数
    #dst：输出图像，可选
    adaptive_threshold = cv2.adaptiveThreshold(gray, 200, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY_INV, 11, 1)
    plt.imshow(adaptive_threshold)
    #行求和，划分成多少行
    horizontal_sum = np.sum(adaptive_threshold, axis=1)
    peek_ranges = extract_peek(horizontal_sum, min_val, min_range)
    line_seg_adaptive_threshold = np.copy(adaptive_threshold)
    #画出每一行字
    for i, peek_range in enumerate(peek_ranges):
        x = 0
        y = peek_range[0]
        w = line_seg_adaptive_threshold.shape[1]
        h = peek_range[1] - y
        pt1 = (x, y)
        pt2 = (x + w, y + h)
        cv2.rectangle(line_seg_adaptive_threshold, pt1, pt2, 255)

    vertical_peek_ranges2d = []
    for peek_range in peek_ranges:
        start_y = peek_range[0]
        end_y = peek_range[1]
        line_img = adaptive_threshold[start_y:end_y, :]
        vertical_sum = np.sum(line_img, axis=0)

        vertical_peek_ranges = extract_peek(
            vertical_sum, min_val, min_range)
        vertical_peek_ranges2d.append(vertical_peek_ranges)

    cutImage(img, peek_ranges)

split/origin/TV~{G4`PBZ[1_(FLC76[}12.png
26 90
13 56
87 134
165 212
243 283
314 375
406 454
485 530
555 607
646 691
730 772
预测结果
['不', '丁', '丈', '万', '丈', '丈', '上', '下', '不', '与']


/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
  (prop.get_family(), self.defaultFamily[fontext]))

png

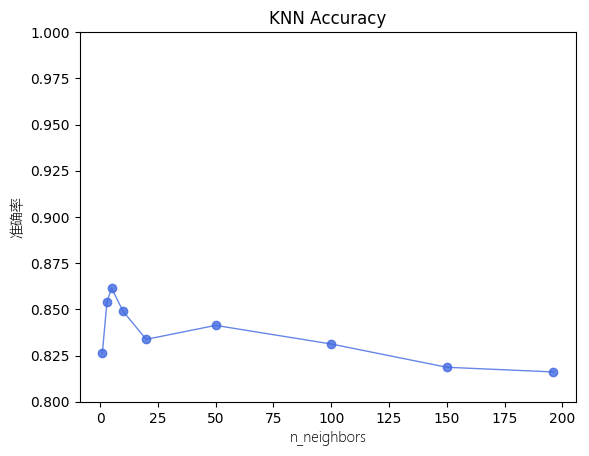
6.8 KNN模型效果测试

from sklearn.neighbors import KNeighborsClassifier
from matplotlib import font_manager
font = font_manager.FontProperties(fname='MSYHL.TTC')
k_list=[1,3,5,10,20,50,100,150,196]
result_list=[]
for i in k_list:
    knn = KNeighborsClassifier(n_neighbors=i)
    # 调用fit()
    knn.fit(x_train, y_train)
    # 预测测试数据集，得出准确率
    y_predict = knn.predict(x_test)
    sum=0
    for j in range(len(y_predict)):
        if y_predict[j]==y_test[j]:
            sum=sum+1
    result_list.append(sum/len(y_predict))
plt.plot(np.array(k_list), result_list, 'ro-', color='#4169E1', alpha=0.8, linewidth=1)
plt.title('KNN Accuracy')
plt.xlabel('n_neighbors', fontproperties=font)
plt.ylabel('准确率', fontproperties=font)
plt.ylim(0.8,1.0)#y轴范围设置
plt.show()

/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/font_manager.py:1331: UserWarning: findfont: Font family ['sans-serif'] not found. Falling back to DejaVu Sans
  (prop.get_family(), self.defaultFamily[fontext]))

png

7.实验结果分析

关于pca降维，虽然135维能保留绝大部分特征，但是后面的曲线增长曲线其实并不算很小，因此降维后的准确率下降也是情有可原，但是识别手写汉字对于精确度要求高，因此其实pca降维在这里并不是一件必要的事情，当资源足够时，不降维更好。
关于SVM准确率，核函数一定要选择rbf，其他两种对于非线性可分的数据集，尤其是手写汉字这种，表现的十分差。在调试参数的时候我发现惩罚系数在0.8-1.0之间准确率都没有很大的差别。
关于KNN和SVM的模型效果对比，可见KNN模型效果准确率时钟低于0.9，在手写汉字这种数据集上表现不佳。