机器学习——决策树

2023-07-03

10.2 分支节点的选择方法

任务

现有一个数据集 weekend.txt，目标是预测一个人周末是否出行，所有特征均为二元特征，取值为 0 或 1。其中“status”（目标特征）表示用户的周末是否出行，1 表示出行，0 表示不出行，“marriageStatus”表示申请人是否已婚、“hasChild”表示申请人是否有小孩、“hasAppointment”表示申请人是否有约、“weather”表示天气是否晴朗；

已知信息熵和信息增益的公式为：

$\text{Entropy}(v_i)=-\sum_{i=1}^{n}P(v_i) \cdot log_2P(v_i)$

$InfoGain=Entropy(C)-\sum_{i=1}^{n}\frac{N(v_i)}{N} \cdot Entropy({C}v_i)$

请自定义函数 cal_entropy(data, feature_name)计算以某特征进行划分后的熵。输入参数 data 为 DataFrame，feature_name 为目标特征的名称；
请根据 cal_entropy() 函数计算决策树分支之前的信息熵，保存为 data_entropy；
请自定义函数 cal_infoGain 计算的信息增益，并分别计算 weekend.txt 中各个特征的信息增益，保存为列表 infogains，并依照信息增益度量的方式选择分支节点 best_feature。

预期结果

待完善代码

import numpy as np
import pandas as pd

# 读取数据
weekend_data = pd.read_table('weekend.txt', sep=' ')

## 自定义计算entropy的函数
def cal_entropy(data, feature_name):
    '''
    data : 数据集变量，DataFrame类型
    featue_name : 目标特征名称
    '''
    
    ## 声明数据集的熵
    entropy = 0
    
    ## 获取data的样本数num
    num = data.shape[0]
    
    ## 使用value_counts()函数获取目标特征`feature_name`取值的频数统计信息freq_stats
    freq_stats = data[feature_name].value_counts()

    ## 遍历目标特征的取值频数
    for index in range(len(freq_stats)):
        
        ## 获取具体的取值频数freq
        freq = freq_stats[index]
        
        ## 通过频数计算频率prob 
        prob = freq / float(num)
        
        ## 计算某个取值的entropy，
        entropy = entropy + (-prob*np.log2(prob))
    
    ## 返回结果
    return round(entropy, 3)

## 调用cal_entropy函数
data_entropy = cal_entropy(weekend_data,'status')

## 自定义计算信息增益的函数cal_infoGain
## data: 数据集变量，DataFrame类型
## base_entropy: 数据集的熵
def cal_infoGain(data, base_entropy):
    
    ## 声明数据集特征的信息增益列表
    infogain_list = []
    
    ## 数据集关于特征的熵
    entropy_list = []
    
    ## 获取数据集的样本数nums, 维度dims
    nums=data.shape[0]
    dims=data.shape[1]
    
    ## 获取数据集的特征名称，类型为list
    feature_list = list(data.columns.values)
    ## 移除目标特征名称
    feature_list.remove('status')
    
    ## 遍历每个特征
    for feature in feature_list:
        
        ## 保存feature不同取值的加权熵
        sub_entropy = 0
        
        ## 切片数据集，获取特征feature的数据记录feature_data 
        feature_data = data[feature]
        
        ## 使用value_count()函数获取特征feature取值的统计信息freq_stats
        freq_stats = data[feature].value_counts()

        ## 获取freq_stats的索引信息，即是feature不同的取值，类型为ndarray
        value_stats=freq_stats.index

        ## 通过列表推导式计算feature各个取值出现的概率feature_prob
        feature_prob = [i/float(nums) for i in freq_stats]
        ## 遍历feature的每个取值以及取值出现的概率
        for pair_value in zip(value_stats, feature_prob):
            
            ## feature取值
            feature_value = pair_value[0]
            ## feature_value出现的概率
            feature_prob = pair_value[1] 
            
            ## 对数据集data切片，获取特征feature取值为feature_value的数据样本sliced_data，类型为DataFrame
            sliced_data=data[data[feature] == feature_value]

            ## 使用cal_entropy函数计算sliced_data的熵entropy
            entropy = cal_entropy(sliced_data,'status')
        
            ## 累加featue取值的熵
            sub_entropy = sub_entropy + feature_prob*entropy
        
        ## 保存sub_entropy到entropy_list中
        entropy_list.append(sub_entropy)   
    
    ## 遍历entropy_list
    for value in entropy_list:
            
        ## 计算信息增益
        infogain=base_entropy-value

        ## infogain取值保留小数点后4位，保存到infogain_list中
        infogain_list.append(round(infogain, 4))
    
    ## 获取infogain_list的最大值max_infogain
    max_infogain=max(infogain_list)

    ## 获取最大值所在的位置索引max_index
    max_index=infogain_list.index(max_infogain)

    ## 根据max_index在feature_list中找到特征的名称best_feature
    best_feature=feature_list[max_index]
    
    ## 返回结果
    return infogain_list, best_feature

## 调用cal_infogain计算各个特征的信息增益infogains，并获取最优的分支节点名称best_feature
infogains, best_feature = cal_infoGain(weekend_data, data_entropy)

## 打印
print (u'信息增益列表：', infogains)
print ('')
print (u'最优的分支节点名称：', best_feature)

信息增益列表： [0.0076, 0.0076, 0.0322, 0.0868]

最优的分支节点名称： weather

10.3 常见的决策树算法

任务

现在有一份有关商品销量的数据集product.csv，数据集的离散型特征信息如下：

特征名称	取值说明
天气	1：天气好；0：天气坏
是否周末	1：是；0：不是
是否有促销	1：有促销；0：没有促销
销量	1：销量高；0：销量低

请根据提供的商品销量数据集 data，使用 sklearn 中的 DecisionTreeClassifier()函数构建决策树模型，模型选择分支节点的度量方式为信息熵
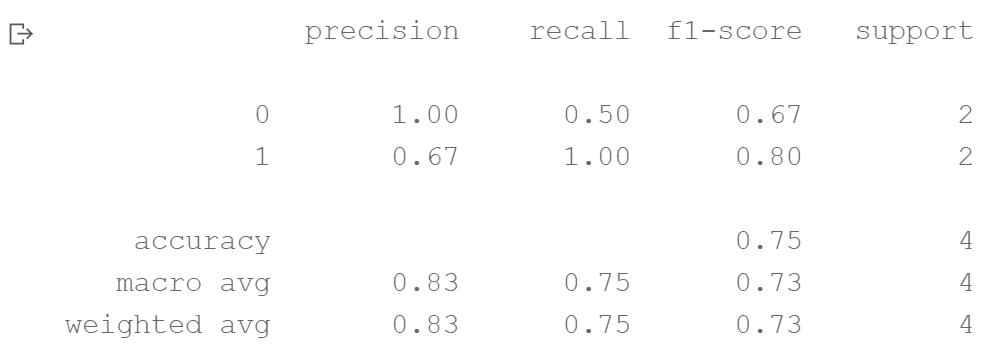
根据模型对 test_X 进行预测，将预测结果存为 pred_y

预期结果

待实现代码

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report

data = pd.read_csv('product.csv')

## 构建分支节点选择方法为信息熵的决策树模型tree_model
tree_model = DecisionTreeClassifier(random_state=3) # 初始化

## 对数据集切片，获取除了目标特征的其他特征的数据记录X
X = data.iloc[:, data.columns != '销量']

## 对数据集切片，获取目标特征`销量`的数据记录y
y = data['销量']

## 使用train_test_split函数划分训练集train_X, train_y和测试集test_X, test_y
## 测试集所占比例为0.1,random_state为0
train_X, test_X, train_y, test_y = train_test_split(X, y, test_size = .1, random_state = 0)

## 拟合数据集
tree_model.fit(X, y)

## 使用tree_model对测试集test_X进行预测判别，获取预测的结果为pred_y
pred_y = tree_model.predict(test_X)

## 使用classification report函数对模型进行评价，并打印函数返回的结果
print (classification_report(test_y, pred_y))

              precision    recall  f1-score   support

           0       1.00      0.50      0.67         2
           1       0.67      1.00      0.80         2

    accuracy                           0.75         4
   macro avg       0.83      0.75      0.73         4
weighted avg       0.83      0.75      0.73         4